SCIP comes along with a set of useful tools that allow to perform automated tests. The following is a step-by-step guide from setting up the test environment for evaluation and customization of test runs.
Setting up the test environment
At first you should create a file listing all problem instances that should be part of the test. This file has to be located in the the directory scip/check/testset/ and has to have the file extension .test, e.g., testrun.test, in order to be found by the scip/check/check.sh script.
All test problems can be listed in the test-file by a relative path, e.g., ../../problems/instance1.lp or absolute path, e.g., /home/problems/instance2.mps in this file. Only one problem should be listed on every line (since the command cat is used to parse this file). Note that these problems have to be readable for SCIP in order to solve them. However, you can use different file formats.
Optionally, you can provide a solution file in the scip/check/testset/ directory containing known information about the feasibility and the best known objective values for the test instances. SCIP can use these values to verify the results. The file has to have the same basename as the .test-file, i.e., in our case testrun.solu. One line can only contain information about one test instance. A line has to start with the type of information given:
=opt= stating that a problem name with an optimal objective value follows=best= stating that a problem name with a best know objective value follows=inf= stating that a problem name follows which is infeasible
With these information types you can encode for an instance named instance1.lp the following information:
- The instance has a known optimal (objective) value of 10.
- The instance has a best known solution with objective value 15.
- The instance is feasible (but has no objective function or we don't know a solution value)
- The instance is infeasible.
If you don't know whether the instance is feasible or not (so the status is unknown), you can omit the instance in the solu-file or write
Note that in all lines the file extension of the file name is omitted.
See the files scip/check/testset/short.test and scip/check/testset/short.solu for an example of a test-file and its corresponding solu-file.
Starting a test run
in the SCIP root directory. Note that testrun is exactly the basename of our test-file (testrun.test). This will cause SCIP to solve our test instances one after another and to create various output files (see Evaluating a test run).
Evaluating a test run
During computation, SCIP automatically creates the directory scip/check/results/ (if it does not already exist) and stores the following output files there.
*.out - output of stdout *.err - output of stderr *.set - copy of the used settings file
*.res - ASCII table containing a summary of the computational results *.tex - TeX table containing a summary of the computational results *.pav - PAVER output
The last three files in the above list, i.e., the files containing a summary of the computational results, can also be generated manually. Therefore the user has to call the evalcheck.sh script in the check directory with the corresponding out file as argument. For example, this may be useful if the user stopped the test before it was finished, in which case the last three files will not be automatically generated by SCIP.
The last column of the ASCII summary table contains the solver status. We distinguish the following statuses: (in order of priority)
- abort: solver broke before returning solution
- fail: solver cut off a known feasible solution (value of the
solu-file is beyond the dual bound; especially if problem is claimed to be solved but solution is not the optimal solution) or if a final solution check revealed a violation of one of the original constraints.
- ok: solver solved problem with the value in solu-file
- solved: solver solved problem which has no (optimal) value in solu-file (since we here cannot detect the direction of optimization, it is possible that a solver claims an optimal solution which contradicts a known feasible solution)
- better: solver found solution better than known best solution (or no solution was noted in the
solu-file so far)
- gaplimit, sollimit: solver reached gaplimit or limit of number of solutions (at present: only in SCIP)
- timeout: solver reached any other limit (like time or nodes)
- unknown: otherwise
Additionally the evalcheck.sh script can generate a solu-file by calling
./evalcheck.sh writesolufile=1 NEWSOLUFILE=<solu-file> <out-file>
where <solu-file> denotes the filename of the new file where the solutions shall be (and <out-file> denotes the output (.out) files to evaluate).
Another feature can be enabled by calling:
./evalcheck.sh printsoltimes=1 ...
The output has two additional columns containing the solving time until the first and the best solution was found.
Note: The basename of all these files is the same and has the following structure which allows us to reconstruct the test run:
check.<test name>.<binary>.<machine name>.<setting name>
- <
test name> indicates the name of the the test file, e.g., testrun
- <
binary> defines the used binary, e.g., scip-3.2.0.linux.x86_64.gnu.opt.spx
- <
machine name> tells the name of the machine, e.g., mycomputer
- <
setting name> denotes the name of the used settings, e.g., default means the (SCIP) default settings were used
Using the examples out of the previous listing the six file names would have the name:
check.testrun.scip-1.1.0.linux.x86.gnu.opt.spx.mycomputer.default.<out,err,set,res,tex,pav>
Using customized setting files
It is possible to use customized settings files for the test run instead of testing SCIP with default settings. These have to be placed in the directory scip/settings/.
Note: Several common user parameters such as, e.g., the time limit and node limit parameters, cannot be controlled by the settings file, whose specifications would be overwritten by optional command line arguments to the make test command, see Advanced options for a list of available advanced testing options that have to be specified from the command line.
Note: Accessing settings files in subfolders of the settings directory is currently not supported.
To run SCIP with a custom settings file, say for example fast.set, we call
make TEST=testrun SETTINGS=fast test
in the SCIP root directory. It is possible to enter a list of settings files as a double-quoted, comma-separated list of settings names as fast above, i.e. SETTINGS="fast,medium,slow" will invoke the solution process for every instance with the three settings fast.set, medium.set, slow.set before continuing with the next instance from the .test-file. This may come in handy if the whole test runs for a longer time and partial results are already available.
Advanced options
We can further customize the test run by specifying the following options in the make call:
CONTINUE - continue the test run if it was previously aborted [default: "false"] DISPFREQ - display frequency of the output [default: 10000] FEASTOL - LP feasibility tolerance for constraints [default: "default"] LOCK - should the test run be locked to prevent other machines from performing the same test run [default: "false"] MAXJOBS=n - run tests on 'n' cores in parallel. Note that several instances are solved in parallel, but only one thread is used per job (parallelization is not that easy) [default: 1] MEM - memory limit in MB [default: 6144] NODES - node limit [default: 2100000000] TIME - time limit for each test instance in seconds [default: 3600] SETCUTOFF - if set to '1', an optimal solution value (from the .solu-file) is used as objective limit [default: 0] THREADS - the number of threads used for solving LPs, if the linked LP solver supports multithreading [default: 1] VALGRIND - run valgrind on the SCIP binary; errors and memory leaks found by valgrind are reported as fails [default: "false"]
Comparing test runs for different settings
Often test runs are performed on the basis of different settings. In this case, it is useful to have a performance comparison. For this purpose, we can use the allcmpres.sh script in the check directory.
Suppose, we performed our test run with two different settings, say fast.set and slow.set. Assuming that all other parameters (including the SCIP binary), were the same, we may have the following res-files in the directory scip/check/results/
check.testrun.scip-3.2.0.linux.x86_64.gnu.opt.spx.mycomputer.fast.res
check.testrun.scip-3.2.0.linux.x86_64.gnu.opt.spx.mycomputer.slow.res
For a comparison of both computations, we simply call
allcmpres.sh results/check.testrun.scip-3.2.0.linux.x86_64.gnu.opt.spx.mycomputer.fast.res \
results/check.testrun.scip-3.2.0.linux.x86_64.gnu.opt.spx.mycomputer.slow.res
in the check directory. This produces an ASCII table on the console that provide a detailed performance comparison of both test runs. Note that the first res-file serves as reference computation. The following list explains the output. (The term "solver" can be considered as the combination of SCIP with a specific setting file.)
Nodes - Number of processed branch-and-bound nodes. Time - Computation time in seconds. F - If no feasible solution was found, then '#', empty otherwise. NodQ - Equals Nodes(i) / Nodes(0), where 'i' denotes the current solver and '0' stands for the reference solver. TimQ - Equals Time(i) / Time(0). bounds check - Status of the primal and dual bound check.
proc - Number of instances processed. eval - Number of instances evaluated (bounds check = "ok", i.e., solved to optimality within the time and memory limit and result is correct). Only these instances are used in the calculation of the mean values. fail - Number of instances with bounds check = "fail". time - Number of instances with timeout. solv - Number of instances correctly solved within the time limit. wins - Number of instances on which the solver won (i.e., the solver was at most 10% slower than the fastest solver OR had the best primal bound in case the instance was not solved by any solver within the time limit). bett - Number of instances on which the solver was better than the reference solver (i.e., more than 10% faster). wors - Number of instances on which the solver was worse than the reference solver (i.e., more than 10% slower). bobj - Number of instances on which the solver had a better primal bound than the reference solver (i.e., a difference larger than 10%). wobj - Number of instances on which the solver had a worse primal bound than the reference solver (i.e., a difference larger than 10%). feas - Number of instances for which a feasible solution was found. gnodes - Geometric mean of the processed nodes over all evaluated instances. shnodes - Shifted geometric mean of the processed nodes over all evaluated instances. gnodesQ - Equals nodes(i) / nodes(0), where 'i' denotes the current solver and '0' stands for the reference solver. shnodesQ - Equals shnodes(i) / shnodes(0). gtime - Geometric mean of the computation time over all evaluated instances. shtime - Shifted geometric mean of the computation time over all evaluated instances. gtimeQ - Equals time(i) / time(0). shtimeQ - Equals shtime(i) / shtime(0). score - N/A
all - All solvers. optimal auto settings - Theoretical result for a solver that performed 'best of all' for every instance. diff - Solvers with instances that differ from the reference solver in the number of processed nodes or in the total number of simplex iterations. equal - Solvers with instances whose number of processed nodes and total number of simplex iterations is equal to the reference solver (including a 10% tolerance) and where no timeout occured. all optimal - Solvers with instances that could be solved to optimality by all solvers; in particular, no timeout occurred.
Since this large amount of information is not always needed, one can generate a narrower table by calling:
where NodQ, TimQ and the additional comparison tables are omitted.
If the res-files were generated with the parameter printsoltimes=1 we can enable the same feature here as well by calling:
allcmpres.sh printsoltimes=1 ...
As in the evaluation, the output contains the two additional columns of the solving time until the first and the best solution was found.
Statistical tests
The allcmpres script also performs two statistical tests for comparing different settings: For deciding whether more feasible solutions have been found or more instances have been solved to optimality or not, we use a McNemar test. For comparing the running time and number of nodes, we use a variant of the Wilcoxon signed rank test. A detailed explanation can be found in the PhD thesis of Timo Berthold (Heuristic algorithms in global MINLP solvers).
McNemar test
Assume that we compare two settings S1 and S2 with respect to the number of instances solved to optimality within the timelimit. The null hypothesis would be "Both settings lead to an equal number of instances being solved
to optimality", which we would like to disprove. Let 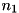 be the number of instances solved by setting
be the number of instances solved by setting S1 but not by S2, and let 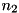 be the number of instances solved by setting
be the number of instances solved by setting S2 but not by S1. The McNemar test statistic is
![\[ \chi^2 = \frac{(n_1 - n_2)^2}{n_1 + n_2}. \]](form_47.png)
Under the null hypothesis, 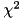 is chi-squared distributed with one degree of freedom. This allows to compute a
is chi-squared distributed with one degree of freedom. This allows to compute a 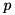 -value as the probability for obtaining a similar or even more extreme result under the null hypothesis. More explicitly,
-value as the probability for obtaining a similar or even more extreme result under the null hypothesis. More explicitly, allcmpres uses the following evaluation:
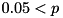 : The null hypothesis is accepted (marked by "X").
: The null hypothesis is accepted (marked by "X").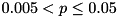 : The null hypothesis might be false (marked by "!").
: The null hypothesis might be false (marked by "!").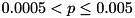 : The null hypothesis can be false (marked by "!!").
: The null hypothesis can be false (marked by "!!").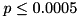 : The null hypothesis is very likely false (marked by "!!!").
: The null hypothesis is very likely false (marked by "!!!").
As an example consider the following output:
McNemar (feas) x2 0.0000, 0.05 < p X
McNemar (opt) x2 6.0000, p ~ (0.005, 0.05] !
Here, x2 represents 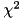 .
.
In this case, the test with respect to the number of found feasible solutions is irrelevant, since their number is equal. In particular, the null hypothesis gets accepted (i.e., there is no difference in the settings - this is marked by "X").
With respect to the number of instances solved to optimality within the timelimit, we have that 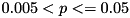 (marked by
(marked by p ~ (0.005, 0.05)). Thus, there is some evidence that the null hypothesis is false, i.e., the settings perform differently; this is marked by "!". In the concrete case, we have 230 instances, all of which are solved by setting S2, but only 224 by setting S1.
Wilcoxon signed rank test
Assume that we compare two settings S1 and S2 with respect to their solution times (within the time limit). We generate a sorted list of the ratios of the run times, where ratios that are (absolutely or relatively) within 1% of 1.0 are discarded, and ratios between 0.0 and 0.99 are replaced with their negative inverse in order to obtain a symmetric distribution for the ratios around the origin. We then assign ranks 1 to N to the remaining N data points in nondecreasing order of their absolute ratio. This yields two groups G1 and G2 depending on whether the ratios are smaller than -1.0 or larger than 1.0 (G1 contains the instances for which setting S1 is faster). Then the sums of the ranks in groups G1 and G2 are computed, yielding values R1 and R2, respectively.
The Wilcoxon test statistic is then
![\[ z = \frac{\min(R1, R2) - \frac{N(N+1)}{4}}{\sqrt{\frac{N(N+1)(2N+1)}{24}}}, \]](form_55.png)
which we assume to be (approximately) normally distributed (with zero mean) and allows to compute the probability 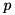 that one setting is faster than the other. (Note that for
that one setting is faster than the other. (Note that for  , we apply a correction by subtracting 0.5 from the numerator).
, we apply a correction by subtracting 0.5 from the numerator).
As an example consider the following output:
Wilcoxon (time) z -0.1285, 0.05 <= p X
Wilcoxon (nodes) z -11.9154, p < 0.0005 !!!
While the 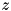 -value is close to zero for the run time, it is extremely negative regarding the solving nodes. This latter tendency for the number of nodes is significant on a 0.05 % level, i.e., the probability
-value is close to zero for the run time, it is extremely negative regarding the solving nodes. This latter tendency for the number of nodes is significant on a 0.05 % level, i.e., the probability 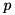 that setting
that setting S1 uses more nodes than setting S2 is negligible (this null hypothesis is rejected - marked by "!!!").
However, the null hypothesis is not rejected with respect to the run time. In the concrete case, setting S1 has a shifted geometric mean of its run times (over 230 instances) of 248.5, for S2 it is 217.6. This makes a ratio of 0.88. Still - the null hypothesis is not rejected.
Testing and Evaluating for other solvers
Analogously to the target test there are further targets to run automated tests with other MIP solvers. These are:
- for cplex
- for gurobi
- for cbc
- for mosek
- for glpk
- for symphony
- for blis
- for gams
make testgams GAMSSOLVER=xyz
Note: This works only if the referred programs are installed globally on your machine.
The above options like TIME are also available for the other solvers.
For cbc, cplex, gams, and gurobi another advanced option is available:
THREADS - number of threads used in the solution process
After the testrun there should be an .out, an .err and a .res file with the same basename as described above.
Furthermore you can also use the script allcmpres.sh for comparing results of different solvers.



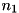 be the number of instances solved by setting
be the number of instances solved by setting 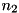 be the number of instances solved by setting
be the number of instances solved by setting ![\[ \chi^2 = \frac{(n_1 - n_2)^2}{n_1 + n_2}. \]](form_47.png)
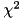 is chi-squared distributed with one degree of freedom. This allows to compute a
is chi-squared distributed with one degree of freedom. This allows to compute a 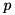 -value as the probability for obtaining a similar or even more extreme result under the null hypothesis. More explicitly,
-value as the probability for obtaining a similar or even more extreme result under the null hypothesis. More explicitly, 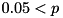 : The null hypothesis is accepted (marked by "X").
: The null hypothesis is accepted (marked by "X").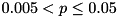 : The null hypothesis might be false (marked by "!").
: The null hypothesis might be false (marked by "!").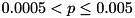 : The null hypothesis can be false (marked by "!!").
: The null hypothesis can be false (marked by "!!").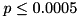 : The null hypothesis is very likely false (marked by "!!!").
: The null hypothesis is very likely false (marked by "!!!").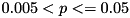 (marked by
(marked by ![\[ z = \frac{\min(R1, R2) - \frac{N(N+1)}{4}}{\sqrt{\frac{N(N+1)(2N+1)}{24}}}, \]](form_55.png)
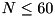 , we apply a correction by subtracting 0.5 from the numerator).
, we apply a correction by subtracting 0.5 from the numerator).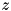 -value is close to zero for the run time, it is extremely negative regarding the solving nodes. This latter tendency for the number of nodes is significant on a 0.05 % level, i.e., the probability
-value is close to zero for the run time, it is extremely negative regarding the solving nodes. This latter tendency for the number of nodes is significant on a 0.05 % level, i.e., the probability